- 표본분포
표본분포(sample distribution) 표본에서 도출되는 통계량에 대한 확률분포이다. 다시 말해, 표본분포는 모수를 추정하기 위한 표본 통계량의 확률분포이다.
필자를 비롯하여 많은 사람들이 표본분포를 '추출된 표본에서 분포를 확인하는 것'이라고 잘못 이해하고 있는 경우가 많다. 표본분포는 '표본 통계량의 확률분포'임을 잊지 말자.
- 표본평균의 오차
표본평균의 오차란 표본으로부터 모수를 추정했을 때, 모수와 통계량(표본평균) 간의 차이를 의미한다.
표본을 추출할 때 정확하게 추출했다 하더라도 오차를 피할 수 없는 경우가 대부분이기에, 이 오차를 줄여나가는 것은 매우 중요하다.
보통, 표본의 개수가 늘어날수록 통계량이 모수와 가까워진다고 말한다.
이를 표본평균의 오차의 관점에서 다시 말하면, 표본의 개수가 늘어날수록 표본평균의 오차가 줄어들어 통계량이 모수와 가까워진다고 표현할 수 있다.
이러한 현상을 뒷받침하는 개념이 있는데, 이것이 통계학의 기반이 되는 중심극한정리이다.
- 중심극한정리(Central Limit Theorem : CLT)
중심극한정리는 표본의 개수(n)가 충분하다면 모수를 모르는 상황에서도 표본 통계량으로 정규분포를 구성하여 모수를 추정할 수 있다는 것이다.
중심극한정리에서는 모집단이 정규분포를 이루지 않아도 표본의 개수가 충분하다면 정규분포를 이룬다고 가정할 수 있다.
- 중심극한정리의 중요성
중심극한정리가 중요한 이유 크게 두가지가 있다.
1. 분포의 비교가 용이해진다.
위의 케이스는 아래의 그림으로 설명할 수 있다.
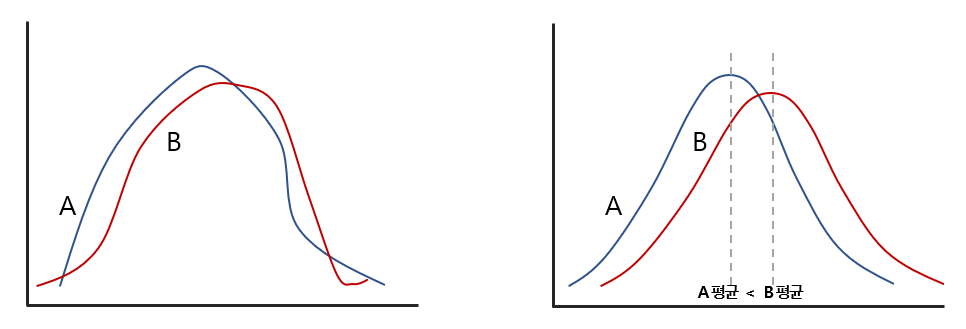
위의 A와 B라는 집단이 있다고 가정할 때, 실제의 분포를 나타낸 그래프로는 한눈에 A와 B의 평균 비교가 어려울 수 있다. 하지만 중심극한 정리를 이용하면 오른쪽과 같이 정규분포 모양으로 분포를 확인할 수 있어 평균의 비교가 용이해진다.
2. 다양한 통계 검정이 가능해진다.
통계학의 많은 모형들은 자료의 분포가 정규분포라는 가정을 필요로 한다.
따라서 모집단의 분포를 알지 못하더라도, 중심극한정리에 의해 표본분포가 정규성을 띈다고 가정할 수 있고, 이로 인해 다양한 확률분포를 통계 검정에 이용할 수 있도록 도와준다.
- 표본의 개수
표본의 개수를 선정하는데에는 어떤 조사를 하는지, 어떤 연구를 하는지 등에 따라 다르다.(즉, 정량적으로 정하기 어렵다는 의미이다.) 보통 통계학에서는 표본의 개수를 최소 30개의 수준으로 필요로 한다고 하지만, 이 개수도 상황에 따라 다른 것을 알 수있다.
통계조사나 설문에서는 표본의 개수를 가능한 한 크게 해야할 필요가 있다. 왜냐하면 모집단의 정보에 대해 확인되지 않은 경우가 대부분이기 때문에 오류를 최대한 방지하고 신뢰성 있는 자료가 되어야 하기 때문이다.
'Data Analysis > Basic statistics' 카테고리의 다른 글
| [기초통계] 확률분포, 이산확률분포 vs 연속확률분포, 이항분포(+베르누이분포), 포아송분포 (0) | 2019.09.06 |
|---|---|
| [기초 통계] 표준화, 정규분포, z분포, t분포, 카이제곱분포, F분포 (0) | 2019.09.04 |
| [기초통계] 확률변수와 확률함수의 관계, 이산 확률변수 vs 연속 확률변수 (0) | 2019.09.04 |
| [기초 통계] 모집단, 모수와 통계량, 표본추출 방법 (0) | 2019.09.01 |
| [기초통계] 통계학이란(통계학 목적, 방법, 추정과 예측의 차이) (0) | 2019.09.01 |


댓글