[ 이전 포스팅 : 연관성 분석 중 상관분석 관련 포스팅 ]
[기초통계] 연관성 분석, 상관분석(공분산, 상관계수)
- 연관성 분석 연관성 분석(association analysis)는 조사 대상에서 수집한 자료의 척도를 기준으로 변수들간의 어떤 관계가 있는지 판단하기 위한 분석 방법이다. 척도를 기준으로 변수간의 연관성을 측정하기 때..
dlearner.tistory.com
앞 포스팅에서 변수들 사이의 연관성을 파악하는 상관분석과 그 연관성의 지표가 되는 상관계수를 알아보았다.
상관계수에 한계가 있다면 변수 사이의 얼마만큼의 연관성이 있는지는 알 수 있지만, 하나의 변수가 변화할 때 다른 변수가 어떻게 변화하느냐에 대한 영향을 알 수 없다는 것이다.
이런 아쉬움을 해결해주는 분석 방법이 회귀분석(Regression)이다. 아래에서 좀 더 자세히 파악해보자.
- 회귀분석이란?
회귀분석(Regression)이란 단순히 변수의 연관성이 있는지 없는지에 대해 검정하는 것에서 더 나아가 어떠한 원인이 어떤 결과를 일으키는지에 대한 인과관계를 파악하는 분석 방법이다.
분석 모델에서 원인이 되어 다른 변수에 영향을 주는 변수를 독립변수(independent variavle)이라 하며, 다른 변수로부터 영향을 받아 결과가 되는 변수를 종속변수(dependent variable)이라 한다. 기본적인 개념이지만 회귀분석에서 자주 언급되므로 잘 짚고 넘어가자.
- 단순회귀분석
단순회귀분석(simple regression analysis)은 독립변수 X가 종속변수 Y에 미치는 영향을 회귀식을 이용하여 분석하는 방법이다. 단순회귀분석을 통해 X와 Y간의 수학적인 방정식이 탄생하게 되고, 이 방정식으로 인해 X를 원인으로 하여 Y가 얼마나 영향을 받는지에 대해 설명이 가능하다.
단순회귀분석은 $\beta_0$을 절편으로 갖고, $\beta_1$을 기울기로 갖는 함수식으로 표현되며, 아래와 같은 식을 도출할 수 있다.
$f(x) = \beta_0 + \beta_1x_1$
하지만 X와 Y에 관해서 현실 데이터로는 정확한 선형식을 도출하기 어렵다. 독립변수 X와 종속변수 Y의 관계는 아래와 같은 조건부 평균식으로 표현할 수 있다.
$E(Y|X) = \beta_0 + \beta_1X_1$
- 잔차
독립변수에 따라 종속변수의 변화하는 정도가 실제 데이터에서는 완벽한 선형은 아니다. 각각의 측정치에 따라서 차이가 발생할 수 있으며, 이 차이를 잔차(residual)라 한다.
잔차(residual)는 조건부 평균 $E(Y|X) = \beta_0 + \beta_1X_1$이 실제로 측정된 Y와 다르게 나타나는 부분을 의미한다. 잔차가 반영된 회귀식은 아래와 같이 표현한다.
$Y = \beta_0 + \beta_1X_1+\epsilon$
이렇게 만든 회귀식을 통해 회귀분석을 실행할 수 있으며, 회귀분석을 통해 모수를 추정할 때는 최소자승법(method of least squares)과 최대우도법(maximum likelihood method)이 가장 널리 사용된다.
- 최소자승법(=최소제곱법)
$\hat{Y_i} = \hat{\beta_0}+\hat{\beta_1}X_i + \hat{\epsilon_i}$는 모든 측정치를 대상으로 추정 회귀선을 나타내는 식이다. 측정치들을 모두 만족하는 회귀선은 존재할 확률은 거의 없다는 것은 모두가 알고 있을 것이다. 따라서 측정치와 가장 차이가 적게 나는, 즉 잔차가 가장 적은 회귀선을 구하는 것을 최선으로 해야 한다. 측정치와 회귀선에 따른 추정값의 차이(잔차)를 그냥 더하게 되면 음수와 양수의 상쇄가 일어나므로, 이 값을 제곱하여 더한 최소의 값을 구한다.
이렇게 잔차의 제곱합 $\sum\hat{\epsilon_i^2}$을 최소로 하는 방법을 최소자승법(method of least squares) 혹은 최소제곱법이라고 부른다.
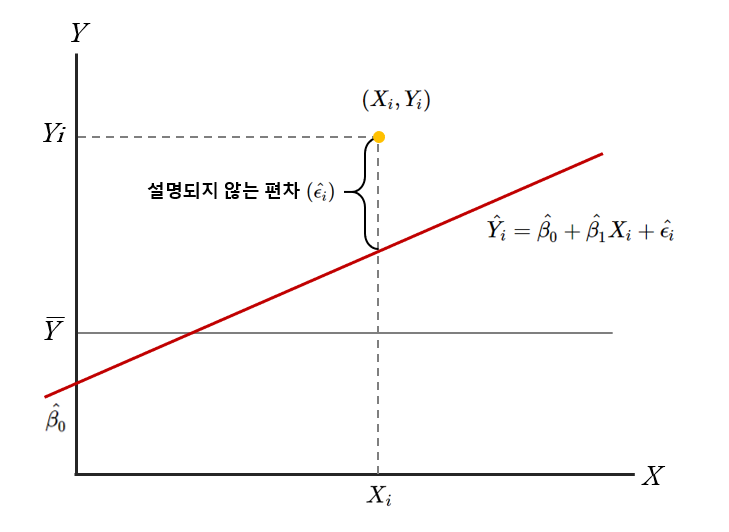
회귀식에서 사용되는 $\hat{\beta_0}$과 $\hat{\beta_1}$은 아래와 같은 과정을 통해 구할 수 있으며, 이를 통해 구해진 $\hat{Y} = \hat{\beta_0}+\hat{\beta_1}X_1$이 가장 잘 추정된 회귀식이라 볼 수 있다.
$\hat{\beta_0}= \bar{Y}-\beta_1\bar{X}$
$\hat{\beta_1}= \frac{\sum(X_i-\bar{X})(Y_i-\bar{Y})}{\sum(X_i-\bar{X})^2}$
'Data Analysis > Basic statistics' 카테고리의 다른 글
| [기초통계] 회귀분석(회귀분석에서의 분산분석 활용, F값, MSE) (0) | 2019.09.23 |
|---|---|
| [기초통계] 회귀분석(적합도 검정, 결정계수) (0) | 2019.09.20 |
| [기초통계] 연관성 분석, 교차분석(교차표, 적합도검정, 독립성검정) (0) | 2019.09.15 |
| [기초통계] 연관성 분석, 상관분석(공분산, 상관계수) (0) | 2019.09.14 |
| [기초통계] 분산분석(ANOVA) (0) | 2019.09.12 |



댓글