앞 포스팅에서 회귀분석의 회귀식을 도출하는 방법을 살펴보았다.
2019/09/17 - [Data Analysis/Basic statistics] - [기초통계] 회귀분석(단순회귀분석, 잔차, 최소제곱법)
[기초통계] 회귀분석(단순회귀분석, 잔차, 최소제곱법)
[ 이전 포스팅 : 연관성 분석 중 상관분석 관련 포스팅 ] [기초통계] 연관성 분석, 상관분석(공분산, 상관계수) - 연관성 분석 연관성 분석(association analysis)는 조사 대상에서 수집한 자료의 척도를 기준으로..
dlearner.tistory.com
이번 포스팅에서는 이렇게 도출된 회귀식이 표본을 얼마나 잘 설명하는지에 대해 확인하는 작업을 실시해보려 한다.
- 회귀분석에서의 적합도 검정
적합도 검정(goodness-of-fit test)은 계수를 구해 도출한 회귀식 $Y = \beta_0 + \beta_1X_1$이 표본의 실제값을 얼마나 잘 설명하는지를 확인하는 방법이다. 추정된 회귀식의 설명력에 대한 척도를 $R^2$(회귀선의 설명력, 결정계수)으로 표현한다.
$R^2$값은 결정계수라고도 부르며 보통 0부터 1사이의 숫자로 나타낸다. 0에 가까울수록 작은 설명력을, 1에 가까울수록 큰 설명력을 가진다고 볼 수 있다. 결정계수는 아래와 같이 계산한다.
$R^2$(결정계수) = $\frac{SSR(회귀제곱합)}{SST(총제곱합)}$
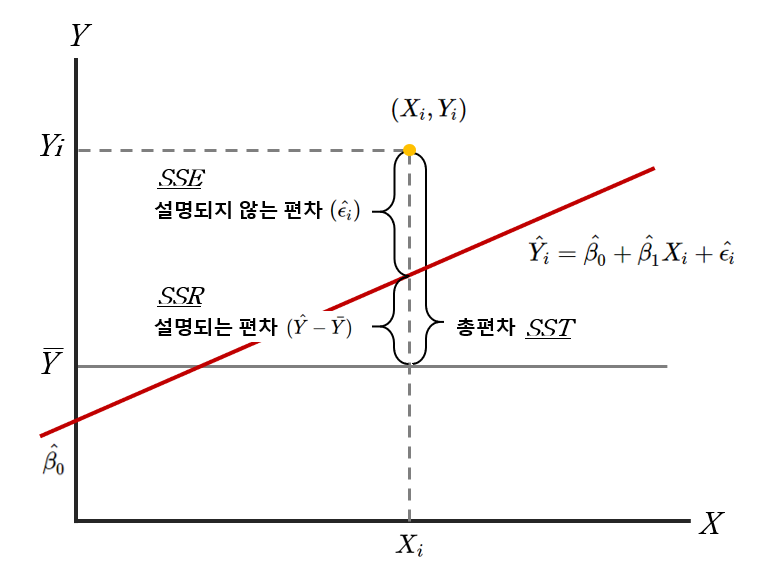
위의 식과 그림에서 결정계수 $R^2$가 뜻하는 바는 총제곱합 중에서 회귀 제곱합이 차지하는 비중이 표본에 대한 회귀식의 설명력을 의미한다. 결정계수 $R^2$은 아래와 같은 변수와 계산식을 통해 계산한다.
|
종속변수 관련 값 |
|||
| $\hat{Y}$ | 예측된 종속변수의 값 | ||
| $\bar{Y}$ | 예측된 종속변수들의 평균값 | ||
| $Y_i$ | 실제 관측치 | ||
|
적합도 검정($R^2$을 계산)을 위한 값 |
|||
|
총편차 |
$Y_i-\bar{Y}$ | 총제곱합(SST) | $\sum{(Y_i-\bar{Y})^2}$ |
| 설명되는 편차 | $\hat{Y}-\bar{Y}$ | 회귀 제곱합(SSR) | $\sum{(\hat{Y}-\bar{Y})^2}$ |
| 설명되지 않는 편차 | $Y_i-\hat{Y}$ | 오차 제곱합(SSE) | $\sum{(Y_i-\hat{Y})^2}$ |
|
$R^2$ 계산 |
|||
|
$SST = SSE + SSR \rightarrow \frac{SSR}{SST}=1-\frac{SSE}{SST}$ |
|||
결정계수는 총편차 중 회귀선으로 설명되는 양을 나타내므로, 설명되는 비율이 높다면 1에 가까워지게 되는 것이다. 또한, SSE가 0에 가까울수록 설명력이 높아진다고도 할 수 있다.
'Data Analysis > Basic statistics' 카테고리의 다른 글
| [기초통계] 회귀분석(회귀 계수의 유의성 검정) (0) | 2019.09.28 |
|---|---|
| [기초통계] 회귀분석(회귀분석에서의 분산분석 활용, F값, MSE) (0) | 2019.09.23 |
| [기초통계] 회귀분석(단순회귀분석, 잔차, 최소제곱법) (0) | 2019.09.17 |
| [기초통계] 연관성 분석, 교차분석(교차표, 적합도검정, 독립성검정) (0) | 2019.09.15 |
| [기초통계] 연관성 분석, 상관분석(공분산, 상관계수) (0) | 2019.09.14 |


댓글